Multivariate Linear Regression

Normal Equation
Gradient descent gives one way of minimizing $J$. Let’s discuss a second way of doing so, this time performing the minimization explicitly and without resorting to an iterative algorithm. In the Normal Equation method, we will minimize $J$ by explicitly taking its derivatives with respect to the $\theta_j$s and setting them to 0. This allows us to find the optimum theta without iteration. The normal equation formula is given below:
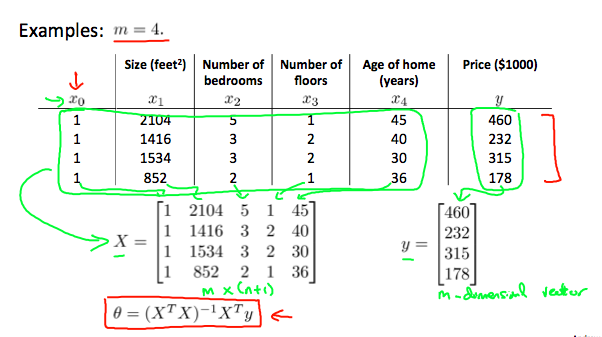
There is no need to do feature scaling with the normal equation.
The following is a comparison of gradient descent and the normal equation:
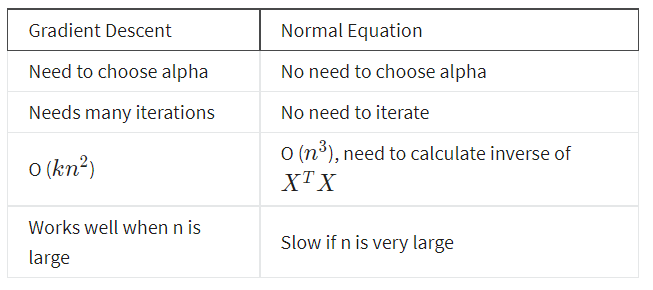
With the normal equation, computing the inversion has complexity $\mathcal{O}(n^3))$.
So if we have a very large number of features, the normal equation will be slow. In practice, when n exceeds 10,000 it might be a good time to go from a normal solution to an iterative process.
Normal Equation Noninvertibility
If $X^TX$ is noninvertible, the common causes might be having:
-
Redundant features, where two features are very closely related (i.e. they are linearly dependent)
-
Too many features (e.g. $m <= n$). In this case, delete some features or use regularization.
Solutions to the above problems include deleting a feature, that is linearly dependent with another or deleting one or more features when there are too many features.