Real World Data
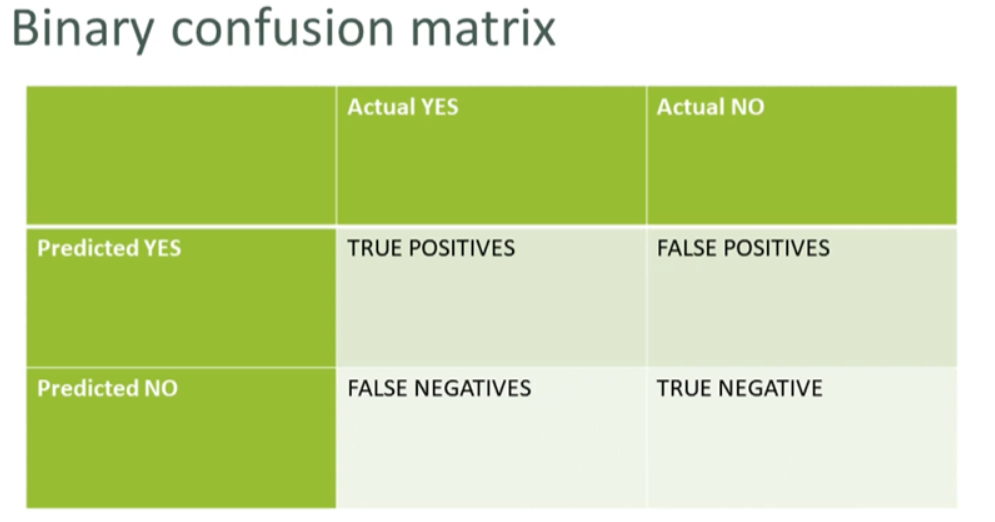
Confusion Matrix
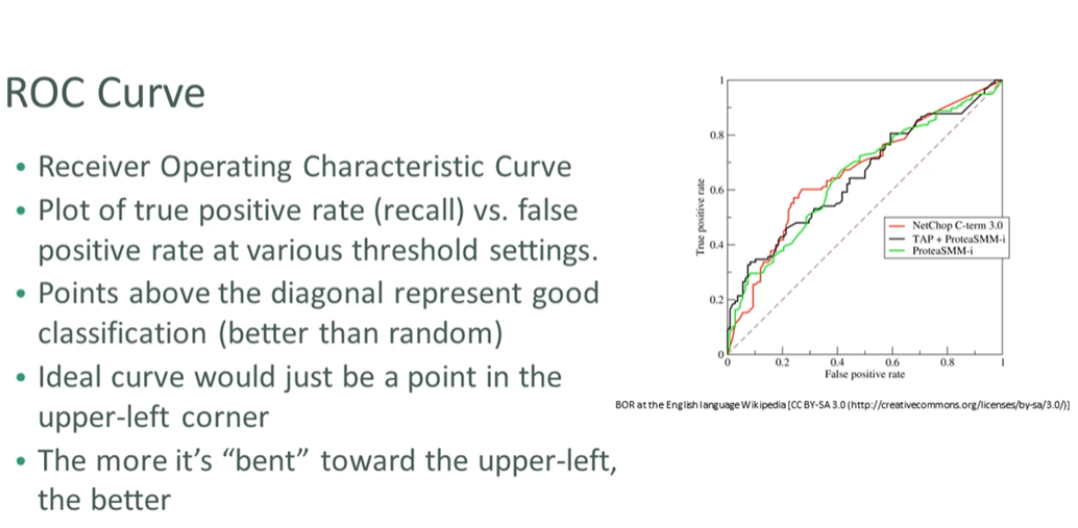
Measuring Classifiers





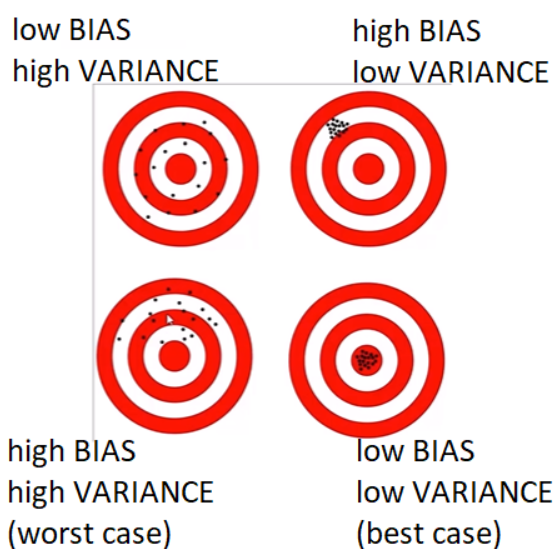
Bias and Variance
BIAS is how far removed the mean of your predicted values is from the “real” answer.
VARIANCE is how scattered your predicted values are from the “real” answer.


-
low variance relative to these observations and high bias
-
high variance, low bias

Increasing K in K-Nearest-Neighbors decreases variance and increases bias (by averaging together more neighbors)
A single decision tree is prone to overfitting - high variance
- but a random forest decreases that variance
K-Fold Cross Validation
- split your data into K randomly-assigned segments
- reserve one segment as your test data
- train on the combined remaining K-1 segments and measure performance against the test set
- repeat for each segment
- take the average of the K-squared scores
import numpy as np
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn import datasets
from sklearn import svm
iris = datasets.load_iris()
X_train, X_test, Y_train, Y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0)
clf = svm.SVC(kernel="linear", C=1).fit(X_train, Y_train)
clf.score(X_test, Y_test)
0.9666666666666667
scores = cross_val_score(clf, iris.data, iris.target, cv=5)
scores
array([0.96666667, 1. , 0.96666667, 0.96666667, 1. ])
scores.mean()
0.9800000000000001
clf = svm.SVC(kernel="poly", C=1).fit(X_train, Y_train)
clf.score(X_test, Y_test)
0.9
Dealing with Outliers
import matplotlib.pyplot as plt
incomes = np.random.normal(27000, 15000, 10000)
incomes = np.append(incomes, [1000000000])
plt.hist(incomes, 50)
plt.show()

incomes.mean()
126959.41748252927
def reject_outliers(data):
u = np.median(data)
s = np.std(data)
filtered = [a for a in data if (u - 2 * s < a < u + 2 * s)]
return filtered
filtered = reject_outliers(incomes)
plt.hist(filtered, 50)
plt.show()
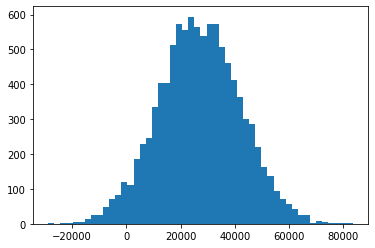
np.mean(filtered)
26972.11342427752

Data

OVERSAMPLING
Duplicate samples from the minrity class
Can be done at random
UNDERSAMPLING
Instead of creating more positive samples, remove negative ones
Throwing data away is usually not the best approach


Binning

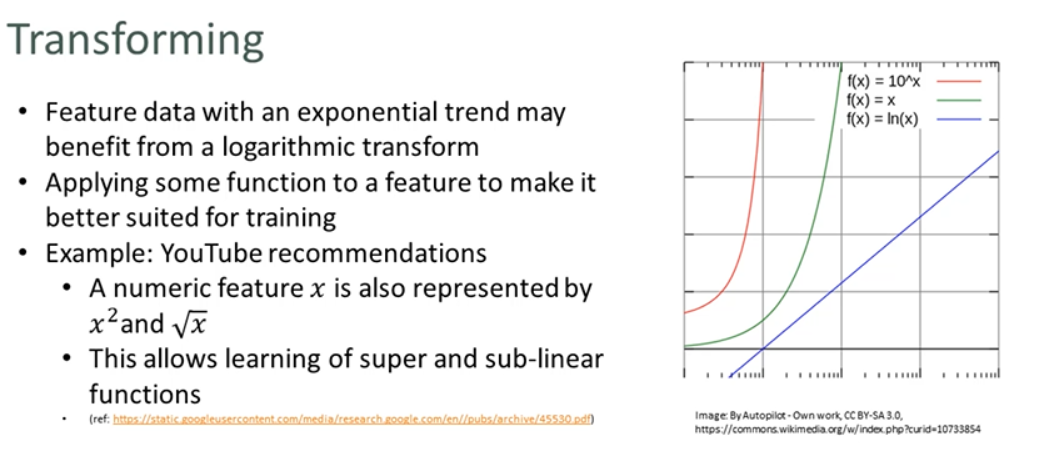
Transforming
Encoding

Scaling / Normalization