Multiclass Classification

Multiclass Classification: One-vs-All
Now, we will approach the classification of data when we have more than two categories. Instead of $y = { 0, 1 }$ we will expand our definition so that $y = { 0, 1 … n }$.
Since $y = { 0, 1 … n }$, we divide our problem into $n + 1$ ($+ 1$ because the index starts at 0) binary classification problems; in each one, we predict the probability that $y$ is a member of one of our classes.
We are basically choosing one class and then lumping all the others into a single second class. We do this repeatedly, applying binary logistic regression to each case, and then use the hypothesis that returned the highest value as our prediction.
The following image shows how one could classify 3 classes:
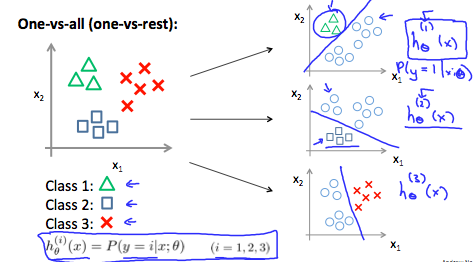
To summarize:
Train a logic regresion classifier $h_{\theta}(x)$ for each class to predict the probability that $y = i$.
To make a prediction on a new $x$, pick the class that maximizes $h_{\theta}(x)$.